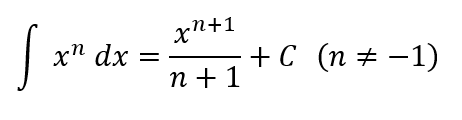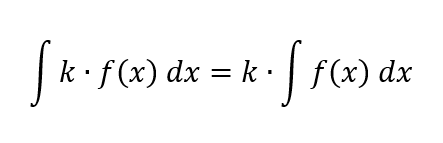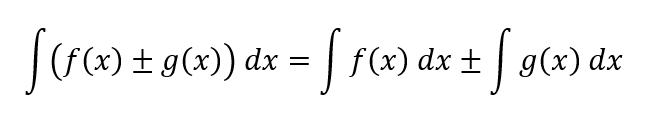Das Thema Integralrechnung spielt eine große Rolle im Mathe-Abitur. Ein Teilbereich der Integralrechnung ist die Berechnung des Unbestimmten Integrals. In diesem Blogbeitrag zeigen wir dir Schritt für Schritt, wie du ein Unbestimmtes Integral berechnen kannst und welche Regeln dabei gelten.
Was ist ein Unbestimmtes Integral?
Wenn du die Ableitung einer Funktion kennst und herausfinden willst, wie die Funktion ursprünglich aussah, musst du ein Unbestimmtes Integral berechnen.
Kurzdefinition: Ein unbestimmtes Integral ist die Menge aller Stammfunktionen einer gegebenen Funktion. Man sagt auch: Das Integrieren ist die Umkehrung der Ableitung.
Beispiel:
Die Ableitung von x² ist 2x. Wenn du also ∫ 2x dx berechnest, kommst du wieder zu x² plus einer kleinen Besonderheit (dazu gleich mehr).
Warum ist das Integral „unbestimmt“?
Beim Ableiten einer Funktion verschwinden alle Konstanten.
Beispiele:
- (x² + 3)' = 2x
- (x² – 5)' = 2x
- (x² + 100)' = 2x
Alle drei Funktionen haben dieselbe Ableitung → 2x.
Beim Integrieren wissen wir also nicht, welche Konstante vorher da war.
Deshalb schreiben wir beim unbestimmten Integral immer + C, wobei C eine beliebige reelle Zahl ist und Integrationskonstante genannt wird.
Wie schreibt man ein Unbestimmtes Integral?
Die allgemeine Schreibweise lautet:
Dabei gilt:
- F(x) ist eine Stammfunktion von f(x).
- C ist die Integrationskonstante.
Die wichtigsten Regeln zur Berechnung des Unbestimmten Integrals
Regel 1: Potenzregel
Die Potenzregel kennst du vom Ableiten – beim Integrieren läuft sie „umgekehrt“. Die Potenzregel sagt:
Wenn du das unbestimmte Integral einer Potenzfunktion berechnest, erhöhe den Exponenten um 1 und teile anschließend durch diesen neuen Exponenten.
Potenzregel:
Beispiele:
Achtung Sonderfall: Die Potenzregel gilt nicht für n = −1.
Merke dir:
Integralrechnung und weitere Abi-Themen üben
Regel 2: Faktorregel
Die Faktorregel des Unbestimmten Integrals erlaubt dir eine Zahl, die vor der Funktion steht, beim Integrieren einfach „vor das Integral zu ziehen“. Das macht die Rechnung viel einfacher, weil du dann nur noch die eigentliche Funktion integrieren musst – ohne den Faktor.
Faktorregel:
Beispiel:
Regel 3: Summenregel
Die Summenregel des unbestimmten Integrals sagt dir, wie du ein Integral berechnest, wenn deine Funktion aus mehreren Summanden besteht – also aus mehreren „Einzelteilen“. Sie erlaubt dir, jeden Summanden einzeln zu integrieren.
Das heißt: Plus bleibt Plus, Minus bleibt Minus und du integrierst jeden Term für sich.
Summenregel:
Beispiel:
Und wofür braucht man Unbestimmte Integrale?
Das Unbestimmte Integral ist nicht nur ein Mathe-Werkzeug – es ist die Grundlage für:
- Flächenberechnung
- Physik (z. B. Geschwindigkeit aus Beschleunigung)
- Wahrscheinlichkeitsrechnung
- Technik und Ingenieurwesen
Mithilfe des Unbestimmten Integrals kannst du aus einer gegebenen Änderungsrate (der Ableitungsfunktion) die ursprüngliche Größe bis auf eine additive Konstante rekonstruieren.
